Conversion analogique-numérique

1. Caractéristiques

On pourra proposer aux élèves d'étudier le principe du CAN à l'aide de LABO_MPI (chaîne de mesure/convertisseur) : CAN [1, 2, 3, 4, 5, 6, 7, 10, 16] et échantillonnage [5, 6, 7, 8].

Un convertisseur analogique-numérique ou CAN transforme une grandeur analogique (tension d'entrée Ue) en une valeur numérique (nombre binaire N en sortie).

Le symbole d’un convertisseur analogique-numérique ou C.A.N. est représenté ci-contre :

le représente la grandeur analogique en entrée
le # représente le mot binaire de sortie codé sur n bits

Rappel :

en binaire : [N]₂ = [ d_n-1 ; d_n-2 ; … d₁ ; d₀ ]
ex. : [N]₂ = [ 1011 ]₂
en décimal : [N]₁₀ = d_n-1.2^n-1 + d_n-2.2^n-2 + … + d₁.2¹ + d₀.2⁰
ex. : [N]₁₀ = 1.2³ + 0.2² + 1.2¹ + 1.2⁰= 8 + 2 + 1 = [ 11 ]₁₀

Un CAN est caractérisé par :

sa plage de tension d'entrée, par exemple de 0 à 5 V (appelé tension pleine échelle)

La plage de tension d'entrée dépend du type de convertisseur : pour un convertisseur unipolaire, elle est par exemple de 0 à 5V ; pour un convertisseur bipolaire, la plage est symétrique autour du 0 , par exemple de :-5 V à 5V .
le nombre de bits du mot de sortie : n = 4, 8, 10, 12, 16, etc...
le pas du convertisseur ou résolution (ou quantum) ; c'est le quotient de la tension pleine échelle par le nombre de mots distincts (2ⁿ pour un convertisseur de 0 à 2ⁿ -1 ). Par exemple pour un CAN 8 bits avec 5 V de tension pleine échelle, on a :

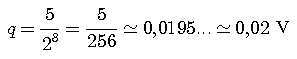
Chaque pas du convertisseur correspond à plusieurs valeurs différentes de la tension ; on peut donc considérer que chaque valeur particulière de la tension analogique donne lieu à un encadrement numérique, par exemple :

3,57422 V < 3,5816 V < 3,59375 V

183 < 3,5816 V <

184

donc la valeur 3,5816 V se situe "entre" le 183^ème et le 184^ème "palier" du CAN utilisé...
On peut convertir en binaire : [183]₁₀ = [10110111]₂

le temps de conversion

2. Echantillonnage

La conversion doit se faire à intervalles de temps réguliers pour suivre les variations de la grandeur à mesurer : cet intervalle de temps est appelé période d'échantillonnage.

La conversion analogique numérique peut donc être décomposée en étapes successives :

1/ On dispose du signal analogique original : c'est la variation de l'amplitude en fonction du temps.

2/ L'échantillonnage consiste à prélever des échantillons du son à intervalles de temps réguliers.

Le nombre de prélèvements en une seconde est appelé fréquence d'échantillonnage.

Plus la fréquence d'échantillonnage est élevée, mieux le signal sera décrit et donc restitué, mais plus le fichier sera volumineux.

3/ On code ensuite les valeurs échantillonnées du signal selon une échelle donnée : c'est la quantification.

Chaque échantillon est comparé à différents seuils : à chaque seuil correspond un code différent ; sur l'exemple suivant on a 16 niveaux possibles, codés sur 4 bits de 0000 à 1111.

Le code correspondant est donc : 0010, 0100, 0101, 0110, 0111, 1000, 1001, 1001, 1001, 1001, 1001, 1000, 1000, 0111, 0111, 0111, 0110, 0110, 0110, 0110...
Dans la réalité le codage se fait sur 8 bits = 1 octet (256 niveaux possibles) ou 16 bits = 2 octets (65736 niveaux possibles).

3. Etude expérimentale

conversion d'une tension continue

Brancher une tension variable (de 0 à 15 V ) sur l'adaptateur Voltmètre et lancer le logiciel Généris : sélectionner Acquisition / MPI / CAN puis Convertisseur (valider 2 fois).

Afficher comme tension de référence la tension maximale que peut délivrer l'alimentation, puis choisir le nombre de bits (de 2 à 12 ) et cliquer sur Convertir pour avoir la valeur en binaire, hexadécimal et décimal.

On peut calculer le pas du convertisseur et essayer de trouver la valeur binaire avant d'effectuer la conversion ; on peut aussi montrer le rôle du nombre de bits du CAN...

étude d'une tension variable : influence du pas du convertisseur (nombre de bits)
On remplace l'alimentation continue par un GBF délivrant un signal sinusoïdal de fréquence 250 Hz (par exemple). On sélectionnera cette fois : Convertir un signal .

Faire l’acquisition pendant une durée de 10 ms sur la voie Directe // ; choisir une fréquence d'échantillonnage de 10 kHz et une résolution de 2 bits : demander la conversion et faire afficher la résolution, puis recommencer pour 4 , 6 , 8 , 10 et 12 bits.

A partir de combien de bits le signal obtenu paraît-il satisfaisant par rapport au signal d’origine ?

étude d'une tension variable : influence de la fréquence d’échantillonnage

Conserver les mêmes réglages du GBF et choisir une résolution de 8 bits. Modifier la valeur de la fréquence d’échantillonnage et demander la conversion pour 250 , 500 , 1000 , 2500 et 5000 Hz (par exemple).

Demander à chaque fois la conversion, afficher la résolution et l’échantillonnage.

Pour obtenir une bonne image de la tension étudiée, il faut une résolution la plus petite possible (et donc un nombre élevé de bits, de préférence > 8 ) et, en général, au moins 10 points de mesure par période.

Le choix de Te est évidemment délicat lorsque l'on ne connaît pas l'ordre de grandeur de la fréquence de la tension étudiée : on choisira dans ce cas la plus grande fréquence d'échantillonnage possible.

4. Application : numérisation du son

Pour numériser fidèlement une valeur ayant une fréquence donnée, il faut numériser au double de cette fréquence. Or l'oreille humaine n'entend pas les sons de fréquence supérieure à 22 000 Hz, ainsi on peut numériser à 44 kHz !
Voici quelques exemples de taux d'échantillonnage et de qualités de son :

Fréquence d'échantillonnage	Qualité du son
44 kHz	CD
22 kHz	radio
8 kHz	téléphone

Trois paramètres interviennent : la fréquence d'échantillonnage, le nombre de bits d'un échantillon et le nombre de voies ( 1 pour la monophonie, 2 pour la stéréophonie, 4 pour la quadriphonie et 6 pour le 5.1 ).

Acquisition de sons avec le magnétophone de Windows :

La carte son incluse dans l’ordinateur est paramétrable en double-cliquant sur l'icone "Réglage du son" (ou sur le haut-parleur présent dans la barre des tâches).
Choisir Options/Propriétés puis sélectionner Lecture et choisir Contrôle du volume/Son/ Synthé SW .
Sélectionner ensuite Enregistrement et choisir Micro (régler le niveau sonore au milieu, sans oublier de sélectionner le micro). Réduire cette fenêtre pour pouvoir éventuellement modifer ces réglages.
Brancher le microphone et le haut-parleur sur la carte son.
Ouvrir le "Magnétophone" de Windows : la fenêtre centrale permet de visualiser l'allure approximative de la tension acquise représentant l’évolution sonore.
Pour acquérir un fichier son, il faut d’abord choisir ses paramètres : l'échantillonnage, le nombre de bits et de voies. Pour cela ouvrir le menu Fichier/Propriétés puis cliquer sur Convertir maintenant ; conserver le format standart proposé PCM mais modifier les attributs d’enregistrement en prenant 44 100 Hz ; 16 bits ; Stéréo .
Acquérir, à l’aide du micro, une petite phrase ou une portion de chant dont la durée est d'environ 5s maximum.
Pour enregistrer le fichier correspondant, ouvrir le menu Fichier/Enregistrer et choisir le chemin suivant : G:\eleves\MPI\44_16_s.wav

A partir de la même acquisition (à recharger à chaque fois), on peut changer les paramètres du fichier enregistré en utilisant comme plus haut Fichier/Propriétés puis Convertir maintenant ; faire ensuite Fichier/Enregistrer sous... avec les paramètres indiqués ci-dessous :

Echantillonnage	Nbre bits	Voies	Durée (s)	Nom fichier	Taille
44 kHz	16	Stéréo	5	44_16_s.wav	861 Ko
44 kHz	8	Stéréo	5	44_8_s.wav	430 Ko
44 kHz	8	Mono	5	44_8_m.wav	215 Ko
22 kHz	8	Mono	5	22_8_m.wav	107 Ko
8 kHz	8	Mono	5	8_8_m.wav	39,1 Ko

Nom fichier	Taille	Modification par rapport au fichier précédent	Comparaison avec le fichier précédent
44_16_s.wav	861 Ko	Modification par rapport au fichier précédent	Comparaison avec le fichier précédent
44_8_s.wav	430 Ko	Nbre de bits / 2	Taille / 2
44_8_m.wav	215 Ko	Mono au lieu stéréo	Taille / 2
22_8_m.wav	107 Ko	fe / 2	Taille / 2
8_8_m.wav	39,1 Ko	fe / 2,75	Taille / 2,74

Calcul théorique de l’encombrement d’un fichier sonore non compressé :

encombrement d’un échantillon : le nombre de bits n doit être exprimé en octets : n / 8
une seconde de son acquis dépend du nombre d’échantillons par seconde fe : n x fe / 8
pour une acquisition de durée totale t, l’encombrement est : t x n x fe / 8
la taille finale de l'extrait dépend du nombre N de voies : N x t x n x fe / 8

Cette "formule" finale correspond-elle aux mesures effectuées ci-dessus ? Justifier.

ex. : 44 kHz 16 bits stéréo pendant 5s : 2 x 5 x 16 x 44000 / 8 = 882 000 octets,
soit en divisant par 1024 : 861,33 Ko (au lieu de 861Ko affichés)

ex. : calculer l’encombrement d’une chanson de 3 minutes à 44 kHz et 16 bits en stéréo.

Le fichier sera 3 x 60 / 5 fois plus gros, soit 30,3 Mo environ. Un CD audio contient environ 700 Mo de données, soit 80 minutes de musique.
Le MP3 ("MPEG Audio layer 3") est un format de compression de données audio qui permet de compresser à un taux de 1:12 les formats audio habituels (WAV ou CD audio) : on peut donc mettre l'équivalent de douze albums de musique sur un seul CD en MP3.
Ce format n'altère pas trop le son pour l'oreille, mais il supprime quelques fréquences inaudibles qui font le "relief" d’un son. L’encombrement d’une chanson de 3 minutes ( 44,1 khz, 16 bits, stéréo ) est alors limité à 30,3/12 = 2,5 Mo, ce qui rend son téléchargement envisageable avec un modem...

5. Etude d'un convertisseur : le CAN Flash

principe :

Ce convertisseur analogique-numérique, encore appelé CAN Parallèle (ou CAN à comparateurs en échelle) permet une grande rapidité de conversion (ce qui permet de l'utiliser par exemple pour les applications vidéo).

Ce type de convertisseur est basé sur l'emploi de 2ⁿ-1 comparateurs associés à un décodeur pour une conversion sous n bits.

ex. :

Nbre de bits du mot de sortie	Nbre de comparateurs nécessaires
2	2² - 1 = 3
3	2³ - 1 = 7
4	2⁴ - 1 = 15
8	2⁸ - 1 = 255

étude d'un CAN Flash à 3 comparateurs

La tension analogique à convertir Ue est appliquée sur l'entrée non inverseuse de chaque comparateur.

La tension de référence Uréf est la tension pleine échelle du convertisseur.

Les résistances R sont identiques, ce qui permet un "découpage" de la tension en intervalles réguliers (quantum).

Pour la compréhension des élèves, il est préférable de prendre des valeurs numériques : on pourra raisonner par exemple avec :

Uréf = 8 V et R = 1000 W

1ère étape : le montage potentiométrique

Calculons la tension U₁ :

soit U₁ =

De même, on trouve :

U₂ =

U₃ =

Calculons la tension U₁ :

soit U₁ = 2 V

De même, on trouve :

U₂ = 4 V

U₃ = 6 V

2ème étape : le comparateur

si Ue > U₁ alors U_A1 = + Usat

si Ue < U₁ alors U_A1 = - Usat

si Ue > 2 V alors U_A1 = + Usat

si Ue < 2 V alors U_A1 = - Usat

Il en va de même pour les deux autres comparateurs : leurs sorties U_A2 et U_A3 vaudront + Usat selon que Ue sera supérieur/inférieur à U₂ ou U₃ .

3ème étape : le décodeur

Chacune des tensions U₁ , U₂ , U₃ est respectivement envoyée sur l'entrée A , B , C d'un circuit logique appelé décodeur, qui transforme en binaire les informations reçues.

Pour simplifier, on notera :

" 0 " la tension - Usat et la tension de sortie nulle du décodeur
" 1 " la tension + Usat et la tension sortie non nulle du décodeur

On peut donc décrire le fonctionnement du décodeur sous la forme d' un tableau :

Ue	Ue	Etat de sortie des comparateurs			Sortie du décodeur
Ue	Ue	C	B	A	d₁	d₀
0 < Ue < Uref / 4	0 < Ue < 2V	0	0	0	0	0
Uref / 4 < Ue < Uref / 2	2V < Ue < 4V	0	0	1	0	1
Uref / 2 < Ue < 3.Uref / 4	4V < Ue < 6V	0	1	1	1	0
3.Uref / 4 < Ue	6V < Ue	1	1	1	1	1

Cette table de vérité est à remplir progressivement avec les élèves, en particulier pour ce qui concerne les sorties (comparateur et décodeur). On peut vérifier pour Ue = 5,6 V (par exemple) en marquant les tensions sur le schéma...

étude d'un CAN Flash à 7 comparateurs

On procède selon les mêmes étapes, de façon à arriver au tableau suivant.

Ue	Ue	Etat de sortie des comparateurs							Sortie du décodeur
Ue	Ue	G	F	E	D	C	B	A	d₂	d₁	d₀
0 < Ue < Uref / 8	0 < Ue < 1V	0	0	0	0	0	0	0	0	0	0
Uref / 8 < Ue < Uref / 4	1V < Ue < 2V	0	0	0	0	0	0	1	0	0	1
Uref / 4 < Ue < 3.Uref / 8	2V < Ue < 3V	0	0	0	0	0	1	1	0	1	0
3.Uref / 8 < Ue < Uref / 2	3V < Ue < 4V	0	0	0	0	1	1	1	0	1	1
Uref / 2 < Ue < 5.Uref / 8	4V < Ue < 5V	0	0	0	1	1	1	1	1	0	0
5.Uref / 8 < Ue < 3.Uref / 4	5V < Ue < 6V	0	0	1	1	1	1	1	1	0	1
3.Uref / 4< Ue < 7.Uref / 8	6V < Ue < 7V	0	1	1	1	1	1	1	1	1	0
7.Uref / 8 < Ue	7V < Ue	1	1	1	1	1	1	1	1	1	1

On peut vérifier pour Ue = 5,6 V (par exemple) en marquant les tensions sur le schéma...

6. Principe d'un voltmètre numérique

On considère un voltmètre numérique dont l'affichage se fait sur 3 chiffres et qui permet d'effectuer des mesures comprises entre 0,00 V et 1,99 V.

Calculons le nombre de bits nécessaire pour le CAN de cet appareil :

tension pleine échelle : Upe = 2,00 V
quantum : q = 0,01 V
nombre de bits : , d'où n = 8 (car 2⁷ < 200 < 2⁸ )
On peut remarquer que le nombre de bits reste le même quelle que soit la gamme de mesures :

Si on veut gagner en précision, il faut un afficheur à 4 chiffres, ce qui modifie le nombre de bits nécessaire pour le CAN :

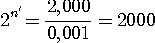, d'où n = 11 (car 2¹⁰ < 2000 < 2¹¹ )