D'après le document www.ac-creteil.fr/physique/DOCGRISP/modulation/modula.htm
publié par l'Académie de Créteil
tpsp9 : Modulation et démodulation
1. Rappels théoriques
- Quelle gamme de fréquences les stations
de radio doivent-elles pouvoir transmettre (voix + musique) ?
- Que se passerait-il si elles émettaient
toutes dans cette gamme ?
- Chaque station se voit affectée une gamme
de (haute) fréquence qui lui est propre, et qui constitue l'onde
porteuse. Comment le signal sonore (de basse fréquence) est-il alors
transmis ?
- Une tension sinusoïdale peut s'écrire :
u(t) =
Umax cos (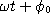 ) = U max cos (2
) = U max cos (2 f t +
f t + 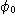 )
)
Que représentent 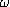 , U max , f
et
, U max , f
et 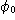 ?
?
On étudie uniquement la modulation
d'amplitude dans le cas où la phase à l'origine est nulle.
On pose :
up(t) = Up cos (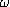 p t) pour
l'onde porteuse
p t) pour
l'onde porteuse
um(t) = Um cos (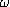 m t) pour
le signal modulant, affecté d'une composante continue U0
.
m t) pour
le signal modulant, affecté d'une composante continue U0
.
On note v(t) l'onde modulée finale : v(t) = [ um(t)
+ U0 ] . up(t)
Montrer que :
v(t) = A [ 1
+ m . cos (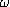 m t ) ] . cos (
m t ) ] . cos (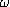 p t)
p t)
Que représentent
A et m ?
Développer l'expression précédente et
montrer que l'on obtient :
v(t) = A cos (2 fp t) + A
fp t) + A 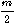 { cos [ 2
{ cos [ 2  (fp - f m) t ] + cos [ 2
(fp - f m) t ] + cos [ 2
 (fp
+ fm) t ] }
(fp
+ fm) t ] }
Le signal modulé correspond donc
à une superposition de 3 signaux de fréquences fp
, (f p - fm) et (fp
+ f m) : représenter le spectre qui correspondrait
à une onde porteuse sinusoïdale de 5000 Hz et à un signal
modulant sinusoïdal de 500 Hz , avec Up = 2 V ; Um
= 4 V ; U0 = 6 V .
2. Modulation d'amplitude (simulation sur tableur)
A partir d'une feuille de calcul vide, on réservera
les trois premières lignes pour l'introduction des paramètres.
Les lignes 4 et 5 seront laissées vides pour "aérer"
la présentation, et la ligne 6 contiendra les titres des colonnes.
La première colonne contiendra une suite de valeurs
de 0 à 1000 représentant une échelle
des temps à partir desquels seront calculées les valeurs
de la porteuse et de la modulation. On calculera ainsi deux périodes
entières de la modulation, ce qui correspond par conséquent à
500 points de calcul par période.
Cette colonne sera créée
en introduisant les valeurs 0 et 1 dans les cellules A7 et A8 , puis en créant
une suite incrémentée jusqu'à la cellule A1007.
La porteuse sera créée
dans la colonne B. L'amplitude de cette porteuse sera choisie égale à
une unité arbitraire, et sa fréquence sera définie relativement
à celle de la modulation, par un facteur multiplicateur introduit dans
la cellule D1 et initialement fixé à 20 par exemple. La formule
à introduire dans la cellule B7 est donc :
=COS(2*PI()/500*$D$1*$A7)
dans laquelle $D$1 définit le multiplicateur de la
fréquence (référence absolue) et $A7 la valeur du
"temps" dans l'échelle de la colonne A (référence
mixte pour faciliter la recopie).
La modulation sera créée
dans la colonne C. Son amplitude sera introduite dans la cellule D2 et initialement
fixée à 0,5 par exemple (sa fréquence étant choisie
par définition égale à une unité arbitraire). La
formule à introduire dans la cellule C7 est donc :
=$D$2*COS(2*PI()/500*$A7)
dans laquelle $D$2 définit l'amplitude (référence
absolue) et $A7 la valeur du "temps".
Le calcul du signal modulé sera effectué
dans la colonne D selon la relation :
La formule à introduire dans la cellule D7
est donc :
=B7*($D$3+C7)
dans laquelle $D$3 définit la valeur du décalage
(référence absolue), B7 et C7 les valeurs de
la porteuse et de la modulation (références relatives).
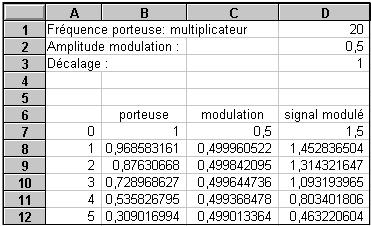
Ces trois formules devront ensuite être recopiées
dans la plage B7 : D1007 de façon à obtenir
le tableau ci-contre. |
|
Il faut maintenant créer le graphique
: il présentera, en fonction du "temps", la modulation et le
signal modulé obtenu, et utilisera les titres définis dans la
ligne 5 pour les séries de données. Il faut donc sélectionner
la plage A6 : D1007 puis lancer l'assistant graphique et choisir une représentation
en "nuage de points" (ne pas oublier de demander la création
du graphique sur une nouvelle feuille pour en améliorer la lisibilité)
.
Il est recommandé de faire varier les trois paramètres
suivants :
- rapport des fréquences porteuse / modulation
(cellule D1)
- amplitude relative de la modulation (cellule D2)
- décalage (composante continue) de la modulation (cellule
D3)
(on remarquera en particulier qu'il se produit une "surmodulation"
lorsque le décalage est insuffisant).
La représentation de la porteuse ne présente
guère d'intérêt et complique le graphique : on peut donc
la supprimer avant d'imprimer les courbes (après avoir légendé
et titré).
3. Démodulation d'amplitude (simulation sur tableur)
A partir d'une feuille de calcul vide, on réservera
les quatre premières lignes pour l'introduction des paramètres.
La ligne 5 sera laissée vide pour "aérer" la présentation
et la ligne 6 contiendra les titres des colonnes.
Comme pour l'étude de la modulation, la première
colonne contiendra une suite de valeurs de 0 à 1000 représentant
une échelle des temps à partir
desquels seront calculées les valeurs de la modulation et du signal modulé.
On calculera ici, afin d'augmenter la lisibilité, une seule période
de la modulation, ce qui correspond par conséquent à 1000 points
de calcul par période. Cette colonne sera créée selon le
processus déjà vu dans l'étude de la modulation.
La modulation sera créée
dans la colonne B, conformément à ce qui a été décrit
précédemment, mais avec une seule période pour 1000 points.
Son amplitude, initialement fixée à 0,5 par exemple, sera introduite
dans la cellule D2. La formule à introduire dans la cellule B7 est donc :
=$D$2*COS(2*PI()/1000*$A7).
Le calcul du signal modulé
sera effectué dans la colonne C, la fréquence relative de la porteuse
étant introduite en D1 et fixée à 100 par exemple, et le
décalage étant introduit en D3 et fixé à 1. La formule
à introduire dans la cellule C7 est donc :
= COS(2*PI()/1000*$D$1*$A7)*($D$3+$B7).
La colonne D contiendra le calcul du signal
redressé : il suffit pour l'obtenir de tester les valeurs
du signal modulé, et de mettre à zéro les valeurs négatives.
La formule à introduire dans la cellule D7 est donc :
=SI(C7>0;C7;0).
La colonne E servira au calcul du signal
filtré , avec une constante de temps définie dans la
cellule D4 et fixée à 100 par exemple (soit une valeur 10 fois
plus grande que la période de la porteuse, mais 10 fois plus petite que
celle de la modulation). Pour cela, on recopiera le contenu de la cellule D7
en E7, et on introduira dans la cellule E8 la formule suivante :
=SI(E7*EXP(-1/$D$4)>D8;E7*EXP(-1/$D$4);D8).
Cette formule a pour but de voir si le signal est en cours
d'augmentation (auquel cas on n'applique pas la loi de décroissance exponentielle)
ou en diminution (auquel cas on applique une décroissance exponentielle
correspondant à la "décharge du condensateur" pendant
une unité de temps). La cellule E7 fait exception car la formule indiquée
ne s'appliquerait pas correctement (référence à la cellule
E6 contenant le titre).
Enfin, il restera à appliquer au résultat un
décalage inverse (suppression de la composante
continue) en introduisant dans la cellule F7 la formule :
=E7-$D$3.
Il faudra ensuite recopier vers le
bas les formules introduites, jusqu'à la ligne 1007, selon
le processus déjà décrit.
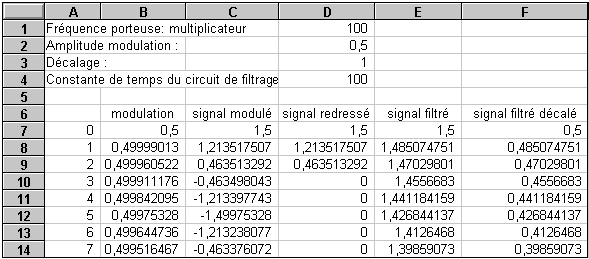
Attention : les formules à recopier
sont celles de la ligne 7, sauf
pour la colonne E pour laquelle
la formule à recopier est en ligne 8. |
|
On pourra alors créer et imprimer les graphiques permettant de suivre
l'évolution du résultat ; pour conserver une bonne lisibilité,
plusieurs graphiques peuvent sembler nécessaire, le dernier pouvant montrer
la ressemblance entre la modulation appliquée initialement et le signal
finalement obtenu.
 f t +
f t +  fp t) + A
fp t) + A 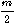 { cos [ 2
{ cos [ 2  (fp - f m) t ] + cos [ 2
(fp - f m) t ] + cos [ 2
 (fp
+ fm) t ] }
(fp
+ fm) t ] }
